08. Sigmoid Function
Here's my solution to the last quiz:
class Linear(Node):
def __init__(self, X, W, b):
# Notice the ordering of the inputs passed to the
# Node constructor.
Node.__init__(self, [X, W, b])
def forward(self):
X = self.inbound_nodes[0].value
W = self.inbound_nodes[1].value
b = self.inbound_nodes[2].value
self.value = np.dot(X, W) + bNothing fancy in my solution. I pulled the value of the X, W and b from their respective inputs. I used np.dot to handle the matrix multiplication.
Sigmoid Function
Neural networks take advantage of alternating transforms and activation functions to better categorize outputs. The sigmoid function is among the most common activation functions.
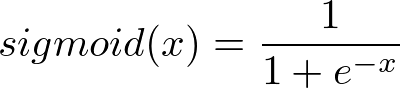
Equation (3)
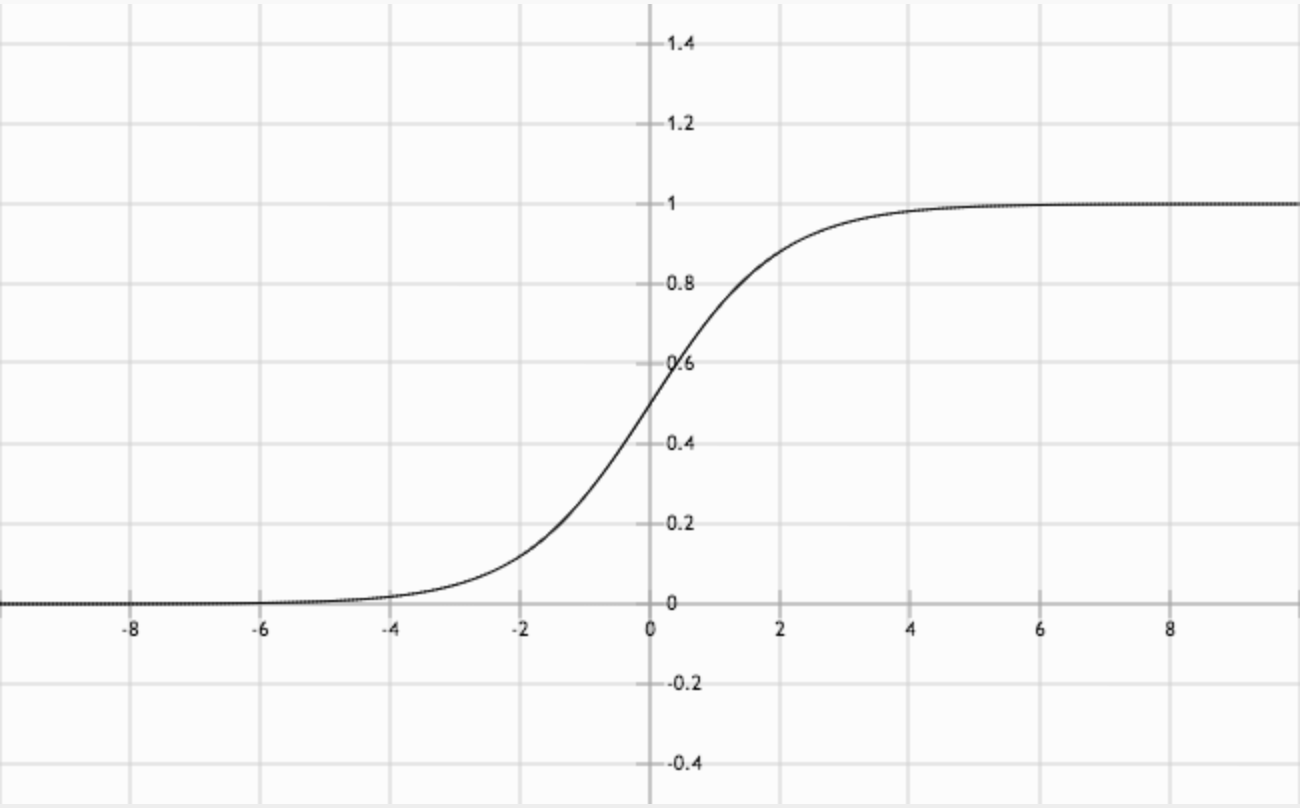
Graph of the sigmoid function. Notice the "S" shape.
Linear transforms are great for simply shifting values, but neural networks often require a more nuanced transform. For instance, one of the original designs for an artificial neuron, the perceptron, exhibits binary output behavior. Perceptrons compare a weighted input to a threshold. When the weighted input exceeds the threshold, the perceptron is activated and outputs 1, otherwise it outputs 0.
You could model a perceptron's behavior as a step function:
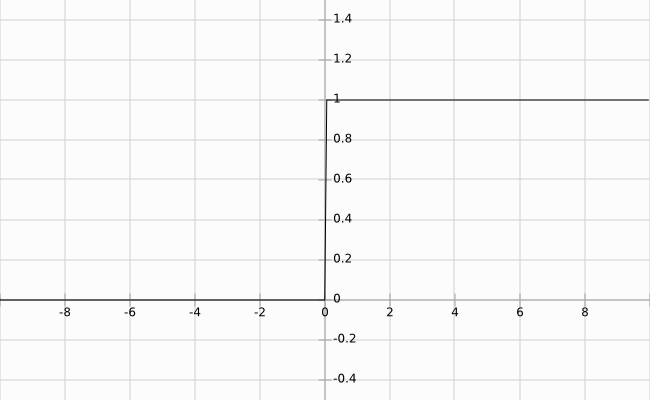
Example of a step function (The jump between y = 0 and y = 1 should be instantaneous).
Activation, the idea of binary output behavior, generally makes sense for classification problems. For example, if you ask the network to hypothesize if a handwritten image is a '9', you're effectively asking for a binary output - yes, this is a '9', or no, this is not a '9'. A step function is the starkest form of a binary output, which is great, but step functions are not continuous and not differentiable, which is very bad. Differentiation is what makes gradient descent possible.
The sigmoid function, Equation (3) above, replaces thresholding with a beautiful S-shaped curve (also shown above) that mimics the activation behavior of a perceptron while being differentiable. As a bonus, the sigmoid function has a very simple derivative that that can be calculated from the sigmoid function itself, as shown in Equation (4) below.
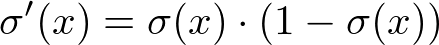
Equation (4). \large \sigma represents Equation (3), the sigmoid function.
Notice that the sigmoid function only has one parameter. Remember that sigmoid is an activation function (non-linearity), meaning it takes a single input and performs a mathematical operation on it.
Conceptually, the sigmoid function makes decisions. When given weighted features from some data, it indicates whether or not the features contribute to a classification. In that way, a sigmoid activation works well following a linear transformation. As it stands right now with random weights and bias, the sigmoid node's output is also random. The process of learning through backpropagation and gradient descent, which you will implement soon, modifies the weights and bias such that activation of the sigmoid node begins to match expected outputs.
Now that I've given you the equation for the sigmoid function, I want you to add it to the MiniFlow library. To do so, you'll want to use np.exp (documentation) to make your life much easier.
You'll be using Sigmoid in conjunction with Linear. Here's how it should look:

Inputs > Linear Transform > Sigmoid
Instructions
- Open nn.py to see how the network will use
Sigmoid. - Open miniflow.py. Modify the
forwardmethod of theSigmoidclass to reflect the sigmoid function's behavior. - Test your work! Hit "Submit" when your
Sigmoidworks as expected.
Question:
Start Quiz: